Estimating Cloud Height
Extra Info For Experts; Not Needed For This Course.
Diagnostics
When air near the ground is humid, cloud base (bottom of clouds) is low for convective clouds. Drier air has higher cloud bases. Here is why.
Cumuliform clouds or convective clouds are formed by warm air rising from near the earth's surface. Picture a blob of rising air called an air parcel. As the air parcel rises, it carries its heat and water molecules with it. But as the air parcel rises, it is moving into altitudes with lower pressure than where it started (because pressure is lower at higher altitudes in the atmosphere). This air parcel expands in the lower pressure, and the expansion causes the air parcel to cool. This process is called adiabatic cooling, because the temperature changes even though there is no heat added or removed from the air parcel (i.e. it is undergoing an adiabatic process). The adiabatic cooling rate for non-cloud air is 9.8 degC for each 1 km of air parcel rise.
But colder air can hold less water as vapor than can warmer air. As the air parcel rises and cools adiabatically, its temperature decreases. Eventually, an altitude is reached where the air parcel is so cold that it can just barely hold the water vapor that it is carrying. This is cloud base, because if the air parcel rises any further, then only a portion of the water molecules could still be held as vapor, forcing the remaining molecules to condense into cloud droplets.

Cumuliform (cumulus mediocris) clouds. Cloud bases (bottom of clouds) are dark, in this high-dynamic range photo.
Two terms are used to estimate cloud base for convective clouds:
- T = Temperature of the air
- Td = Dew-point temperature of the air (a measure of humidity)
Dew point is the temperature that you must cool air at constant pressure in order to get dew or condensation happening. Most of us are familiar with a different way to describe humidity — the relative humidity. Here is how relative humidity and dew point are related: Very humid air, with a relative humidity of 100%, has Td = T. Namely, you don't need to cool the air any amount below the actual air temperature because dew or cloud droplets are already on the verge of forming. As air gets drier, the relative humidity decreases towards 0%, and the dew point becomes colder than the actual air temperature. The greater the difference between the temperature of the air and the dew point temperature, the drier the air. But drier air means you need to lift it higher before it is cold enough for clouds to form.
The height at which a lifted air parcel becomes saturated is called the Lifting Condensation Level (LCL). A quick way to estimate height (zLCL) of the LCL is:
zLCL = a (T – Td)
where a = 0.125 km / degC.
Thus, if you know the near surface T and Td, you can estimate the cloud-base height zLCL above ground level. This height applies to cumuliform clouds (primarily vertical clouds) of all sizes, but does NOT apply to stratiform clouds (primarily horizontal or layer clouds).
If there are enough cumuliform clouds to cover more than 50% of the sky, then the zLCL would be the ceiling.
You can use this method to get a quick estimate of cloud base before you fly. Namely, subtract dew point from temperature (both in degC), and divide the result by 8 to estimate cumulus ceiling in km.
Solved Example
Practice: If T is 20 degC and Td is 14 degC, then what is cloud-base height for convective clouds? Answer: Using the formula
zLCL = a [T – Td]
(0.125 km/degC) x [20 degC – 14 degC]
= (0.125 km/degC) x [6 degC]
= 0.75 km above ground level.
Since pilots usually use feet for altitude, we need to convert this answer, because 1 km = 3280.84 ft. Thus:
zLCL = (0.75 km) x [ (3280.84 ft) / (1 km) ] =2,460.63 ft above ground level.From personal experience, this method of estimating cloud-base height using temperature and humidity is much more accurate than trying to estimate cloud base height by eye (just by looking at the clouds).
Check your understanding
If the air temperature is the same as given above, but the dew-point temperature is warmer, then is cloud base lower, the same, or higher than the previous solution?
How good is the LCL in estimating the height of the actual cloud base of cumuliform clouds? In an earlier life, I did a field experiment in Oklahoma using a laser radar (lidar) to measure the actual cloud-base height. I compared it to the LCL height calculated from T and Td measured at a portable automatic meteorological (PAM) station.
A perfect correlation would be if all the data points fall on the solid diagonal line. The figure below at left shows very good agreement (the different plotted symbols for different days are close to the diagonal line). Namely, the LCL gives a very good estimate of cloud base height as measured with the lidar.
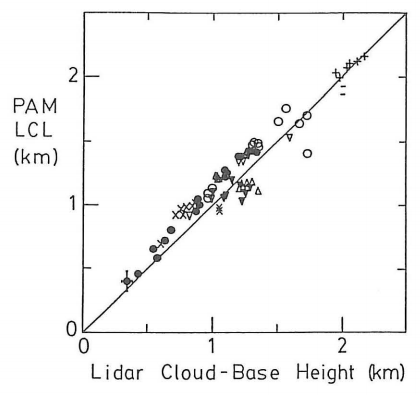
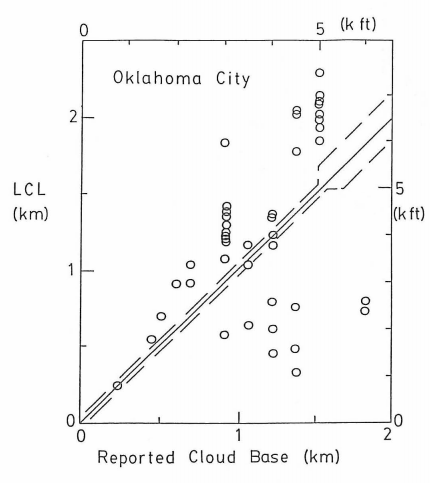
I then compared the LCL with the Reported Cloud Base height from the human weather observers at Oklahoma City airport (see figure at right). The desired accuracy as specified in weather observer manuals is to have the observations as close to the diagonal solid line as possible, but some scatter is OK if the observations are within the dashed lines. Given that the data points fall mostly outside the dashed lines, it appears that even trained weather observers have difficulty in estimating cloud-base height by eye.
Keywords: adiabatic cooling, air parcel, ceiling, cloud base, cumuliform, dew-point temperature, lifting condensation level (LCL)
Image credits. All figures by Roland Stull.