Tutorial 1:
Basics of Understanding and Using Soundings

Intro

Objectives

The focus is on understanding how temperature and humidity layering (vertical structure) of the atmosphere controls thunderstorm intensity and size. To do this, you will learn how to use a graph called a "thermodynamic diagram" (or "thermo diagram" for short), to plot and interpret atmospheric soundings.

Goals:

You will learn and practice how to:

Needed Materials

1) Before coming to this tutorial session, please print and bring with you a few copies of each of the following pages. You can either buy the printed materials from the bookstore as part of the course notes, or can print them for free from the links below.

Printout S1. Thermo-diagram components (pdf)
Printout S2. Comparison of emagram and skew-T diagrams (pdf)
Printout S3. Complete thermo diagram (pdf)

Figure numbers in these Printouts correspond to the figure numbers in the Tutorial, where you can also find the figure captions. You might also want to print out a copy of the Tutorial Activities to bring with you.

2) Also bring some coloured pencils, eraser, and straight edge. If you prefer to use coloured pens instead of pencils, that is fine, but you might want to bring more blank copies of the above figures in case you make mistakes when plotting the graphs.

Method

Activities . The instructor will explain, step-by-step, the different parts of a thermo diagram and how to use them. You should follow along, plotting the examples on your blank copy of Printouts S1 and S2. These step-by-step examples are discussed in detail in the online Tutorial readings. Then, on your own, after the tutorial is finished, you should try doing the similar exercises (B1) that are provided in the Activities link above, to help you gain confidence and understanding in using thermo diagrams. Finally, do similar calculations from real-time soundings you get from the web (B2).

Contents

1. The Environment - Supportive or Oppresive
2. Soundings - to Measure the Environment
3. Air Parcels - Tracking them on Thermo Diagrams
a. Humidity of the Air
b. Rise of Unsaturated Air
c. Rise of Saturated Air
d. Full Thermo Diagram
4. Static Stability (Additional Information - NOT Required)
a. Buoyant Forces
b. Stability Classes
c. How to Determine Layer Stability
d. Interpretation of the Results
5. Predicting Storm Intensity
a. How to Find Parcel Stability
b. Tracking Parcel Rise
c. Convective Inhibition (CIN) and Triggering
d. Convective Available Potential Energy (CAPE)
6. Final Conclusions and Review

Readings for Tutorial 1

1. The Environment - Supportive or Oppressive

Two conditions are needed for a thunderstorm:

To better understand the first condition, we need to understand both the environment around the storm (determined by soundings), and the movement of air parcels through this storm. These are discussed in sections 2 - 4, and then are combined in section 5 to see how storms work.

Thunderstorms need the right environment to form and grow. This is an environment that normally prevents the warm, humid unsaturated boundary-layer air from rising. The boundary layer can thus serve as a reservoir to accumulate the sun's energy, to build up sufficient fuel to power the thunderstorm. However, the environment must allow saturated air to be positively buoyant, so the cloudy air can continue rising on its own once it has been kick started.

An environment that allows saturated, cloud air to rise, but which prevents unsaturated air from rising, is said to be conditionally unstable. To determine this instability, one can measure the existing temperature at different heights in the ambient environment, and compare that to the temperature of a hypothetical blob of air called an air parcel that is "kicked" up from the surface, past the capping inversion, and which rises past its lifting condensation level (LCL) to become saturated (cloudy).

2. Soundings - to Measure the Environment

The measurement of the environmental air at various heights is called a "sounding", or "upper-air data". Soundings are made by attaching meteorological instruments to a radio transmitter, that can relay the observations as the instruments move through the troposphere. Such instruments attached to rising weather balloons are called radiosondes. When dropped with a small parachute from an aircraft, they are called dropsondes. When attached to small weather rockets, they are called rocketsondes. Many commercial aircraft have special instruments to measure the weather and automatically radio the info to ground stations. Satellites can roughly estimate the sounding based on radiation that is emitted from the air at different heights and received by the satellite. Even the time-delay to Global Positioning System (GPS) navigation signals between the GPS satellites and ground stations can be used to infer the temperature and humidity along the path.

Just to make life confusing, the data that are collected from sounding instruments are also called soundings. Also, when this data are plotted on special charts called thermodynamic diagrams, these plots are called soundings. We will focus on these sounding plots.

a. Thermo Diagram Basics: Because pressure always decreases with height, meteorologists use it as a surrogate measure of height. Lower pressures correspond to higher altitudes. So most thermodynamic diagrams (thermo diagrams, for short) have pressure plotted along the vertical axis (decreasing upward on the graph), and temperature plotted along the horizontal axis. Fig 1 shows such a blank graph. Thus, the top of the graph corresponds to higher altitudes, and the right side corresponds to warmer temperatures.

Figure 1

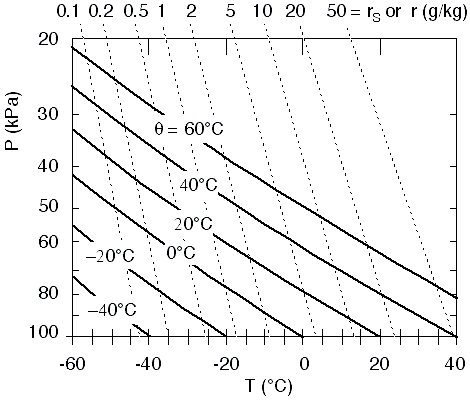
Fig 1. Background for a thermo diagram. Higher in the graph corresponds to higher above ground (where the pressure is lower). P is pressure in kiloPascals (kPa) and T is temperature in degrees Celsius (°C). Horizontal lines are isobars and vertical lines are isotherms. Figure copyright © 2002 by Roland Stull.

In this diagram, along any vertical line the temperature (T) is constant. Hence, these vertical lines are called isotherms (meaning equal temperature), and are labeled in degrees Celsius (°C) at the bottom of each line.

Along any one horizontal line, the pressure (P) is constant. These are called isobars, and are labeled in kiloPascals (kPa) at the left side of each line.

On this blank graph, we can plot the sounding measurements. These measurements are often reported as a temperature and dew point for a variety of heights. For each height, plot two points on the chart: plot a large dot or small circle for T and the plot an "x" for Td. Td is never warmer than T, and can be much colder if the air is very dry. After the points are plotted for each height, draw straight line segments to connect each T point with its closest neighbor, starting from the lowest altitude (bottom of the graph) and working up. This is just a "connect the dots" exercise. Then draw a similar "connect the x's" for the Td data points. Sometimes people use different colour for T and Td. These two lines represent the sounding; namely the T curve represent the environmental temperature, and the Td curve is a measure of the environmental humidity.

Interpretation of a sounding is as follows. First, check that the dew point line never crosses to be warmer than the temperature line, otherwise you probably made a mistake plotting the numbers (or there was an instrument error).

The bottom of the sounding is usually the warmest and has the largest dew point, because of the energy from the sun (sensible and latent heat) being transferred to the air from the ground. The very bottom T and Td are used in the calculation of LCL.

Near the top of the sounding is often a layer of uniform temperature with height (i.e., an isothermal layer). This layer is in the stratosphere, and the bottom of the isothermal layer marks the tropopause (the dividing line between the top of the troposphere and bottom of the stratosphere).

Any regions where T and Td are equal or nearly equal (within about 1°C) indicate layers of clouds. These are stratiform (layered) clouds if aloft, or fog if touching the surface. (To be a cloud, theoretically T must exactly equal Td so that the air is saturated. However, due to instrument errors in the radiosondes, experience has shown that the sonde is probably in a cloud even if the measured Td is within about 1°C of T.) Here are a couple of examples,

b. Plotting Environmental Soundings:

1) Given the following sounding data, plot them on a copy of the blank thermo diagram from Fig 1.

P(kPa)
T(°C)
Td(°C)
20
-30
-60
30
-30
-45
50
-10
-35
65
10
-20
80
25
-5
90
25
20
100
40
25

Table 1. An atmospheric sounding of the environment.

where the bottom measurement is for air touching the surface.

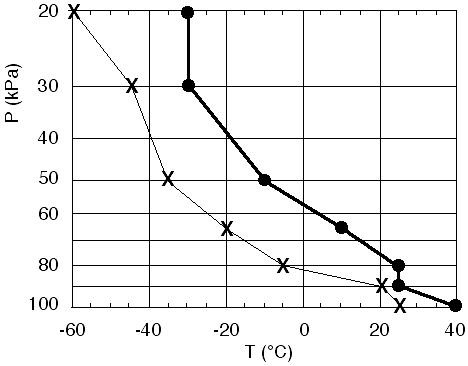
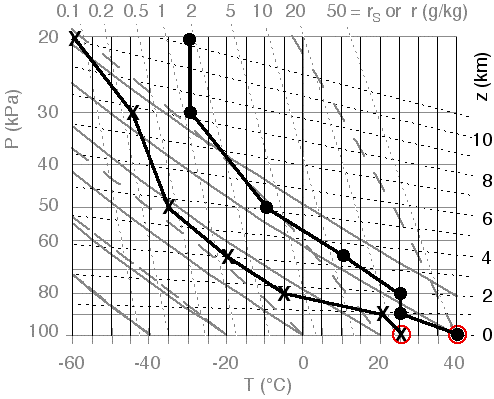
The soundings are plotted in Fig 2, using dots for T, and x's for Td. The boundary layer is the hot humid layer of air between the surface and a height where the pressure is about 85 kPa. The capping inversion is the isothermal layer between 85 and 80 kPa. Below this stable layer is the warm, humid air that can feed a thunderstorm. Above this cap, the air is very dry, as indicated by the large differences between T and Td at each height.

Figure 2

Fig 2. Plot of environmental sounding of Table 1. Dots are temperature (T), and x's are dew-point temperature (Td). Figure copyright © 2002 by Roland Stull.

2) For the sounding from the previous question, what is the value of the LCL (i.e., the altitude of the cloud base), for an air parcel rising from near the surface?

For this calculation, we use only the data closest to the ground. Unless you are told otherwise, assume that the air parcel starts with the same temperature and humidity as the surrounding environmental air at that height (the surface is near P = 100 kPa for this example). Thus, at the surface T = 40°C and Td = 25°C from the table above. Plugging these numbers into the LCL equation (D2) from the "Storm Energy" course notes gives

zLCL = a • (T - Td)
zLCL = (0.125 km/°C) • (40 - 25°C)
zLCL = 1.875 km

3) For the sounding from table 1, where is the tropopause?

There is an isothermal layer of T = -30°C near the top of the sounding, between pressures of 20 and 30 kPa. Thus, the bottom of this layer, at P = 30 kPa, marks the tropopause.

4) At what levels are stratiform clouds, based on the sounding from part (1)?

There are no locations where Td = T in this sounding, so there are no stratiform clouds for this case. The closest approach is at P = 90 kPa, where T = 25 and Td = 20°C.

Try plotting and interpreting a sounding.

3. Air Parcels - Tracking them on Thermo Diagrams

When air parcels move around in thunderstorms, their temperature, pressure, humidity, and amount of condensed water (cloud and rain drops) change. Thermo diagrams were devised so that we could track these changes without having to do any calculations. Instead, we can pick answers off of the diagram. For this reason, thermo diagrams often have more than just isotherms and isobars plotted on them.

We will start with the background thermo diagram of Fig 1, and gradually add more and more lines as we discuss how to use them.

a. Humidity of the Air

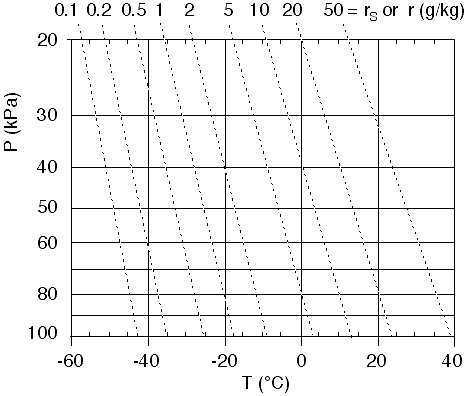
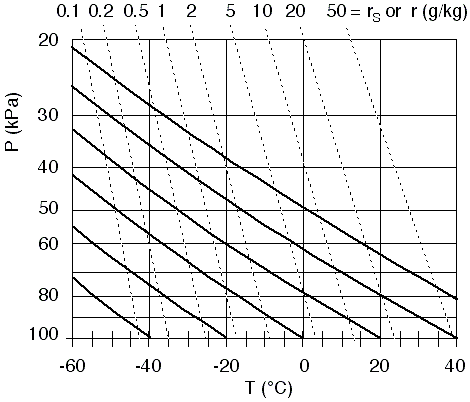
One set of lines that is usually added are isohumes, to aid calculation of humidity. These are shown in Fig 3 as the thin dotted lines (depending on your web browser and the resolution of your screen, these dotted lines might appear as gray solid lines). Isohumes connect locations in the diagram having equal humidity. The humidity value for each isohume is labeled at the top of this thermo diagram as a mixing ratio (r). (Careful! Different thermo diagram manufacturers can put the labels in different places.)

The humidity increases smoothly from lower left to upper right in this diagram. Thus, if you need an isohume that is not plotted on the diagram (such as the 15 g/kg isohume), you should just interpolate smoothly between the two isotherms that are closest (10 and 20 g/kg for Fig 3).

When you do this interpolation for humidity, note that the humidity increases slowly at first from the lower left, but then increases faster and faster as you approach the upper right corner of the graph. Take this variation into consideration when you interpolate.

When using the isohumes in a thermo diagram, the following rules apply. For any point representing temperature, the isohume that goes through that point tells you the saturation mixing ratio, rs. For any point representing dew-point temperature, the isohume that goes through that point tells you the actual mixing ratio, r.

Figure 3

Fig 3. Blank thermo diagram with isohumes (thin dotted lines or gray lines depending on your screen resolution, connecting points of equal humidity). The humidity values are mixing ratio (r) in units of gwater/kgair , as indicated at the top of the graph. Figure copyright © 2002 by Roland Stull.

Let's look at a couple of examples.

1) For the bottom measurement from the previous solved example (P = 100 kPa, T = 40°C, Td = 25°C), first plot them in Fig 3.
2) find the actual mixing ratio value (r).
3) find the saturation mixing ratio (rs).
4) find the relative humidity (%).

Answers:

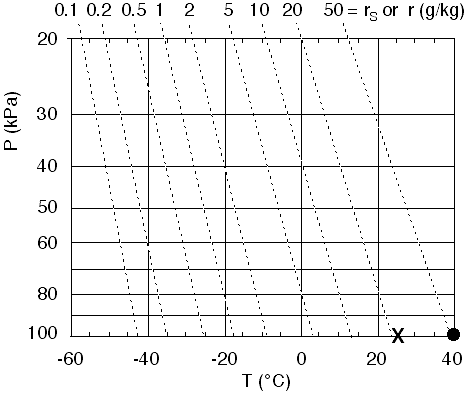
1) The same two points from the bottom of the previous solved example are plotted in Fig 3, as reproduced as Fig 4 here.

Figure 4

Fig 4. Plotting T and Td . Figure copyright © 2002 by Roland Stull.

2) For the dew point measurement (plotted as the X), this point is slightly to the right of the 20 g/kg isohume. So I will guess r = 21 g/kg for the actual mixing ratio. (Just to give me confidence, I double checked using the humidity equations, and found r = 20.83 g/kg for T=25°C at P=100 kPa.)

3) For the temperature measurement (plotted as the dot), the dot is slightly to the right of the 50 g/kg isohume. By eye-balling it, we might guess about rs = 52 g/kg. (It is difficult to tell exactly from this graph, but I cheated by calculating rs based on the equations presented and got an answer of rs = 52.15 g/kg, using T = 40°C at P = 100 kPa.)

4) The thermo diagram does not give RH% directly. However, because we can get both r and rs from it, we can use the definition

RH% = 100 • r / rs = 100 • (21 / 52)
RH% = 40.4%

b. Rise of Unsaturated Air Parcels

So far, we have focused on the state of the air. Namely, its temperature, pressure, and humidity. Just a reminder: it takes 2 points on a thermo diagram to represent that state of 1 air parcel. For example, the T and Td points plotted as the dot and X in the previous solved example represent the one air parcel near the ground. As we saw from that solved example, the state of that air parcel was (P = 100 kPa, T = 40°C, and r = 21 g/kg).

But thunderstorm circulations move air parcels about and change their state; hence, we will now look at processes that change the state of the air. Thermo diagrams can have extra lines added to them to indicate processes (so that we can just pick the numbers off the diagram, instead of calculating them).

Consider unsaturated air parcels that rise from the surface under a thunderstorm. The following rules apply to a rising air parcel:

The second rule above is easy. Since we already have isohumes plotted on these diagrams, and since an isohume represents constant mixing ratio, all we need to do is to move the X (representing the humidity of the parcel) up along, or parallel to, the thin dotted isohumes.

For the first rule, however, we need to add another set of lines, called dry adiabats. These are shown in Fig 5 as the thick diagonal lines (where I have temporarily removed the isotherms and isobars to help reduce clutter). These are lines of constant potential temperature, which has the symbol theta (). Often, thermo diagrams don't put labels on these adiabats, because it is understood that their temperature value is that where it crosses the P=100 kPa isobar, near the bottom of the diagram.

These dry adiabats show the dry adiabatic lapse rate Gd , except using pressure P as the surrogate measure of height z.

The rule for using these dry adiabats is as follows: For a rising or sinking air parcel that is not saturated (not cloudy), the temperature of that air parcel changes by following along (or parallel to) the dry adiabats. Namely, if a dot represents the temperature T of an air parcel starting at some initial pressure height P, then move that dot along (or parallel to) a diagonal line. Stop moving it when you get to the desired different pressure level. The new location of this dot within the thermo diagram indicates its new temperature.

The two rules [temperature (T) cools dry adiabatically, and actual mixing ratio (r) remains constant] can be used together, to find the lifting condensation level (LCL). Remember that the LCL is nothing more than cloud base, where the rising air parcel finally cools so much that water vapor starts condensing out to make cloud droplets.) The rule for finding the LCL is:

Finally, see Fig 6, which is just like Fig 5 except the isotherms and isobars are retained. This is the form that most people would actually use.

Figure 5

Fig 5. Thermodynamic diagram with all lines removed except the isohumes (thin dotted lines representing mixing ratio, r, labeled at the top), and the dry adiabats (thick diagonal lines, labeled as potential temperature or theta ). Figure copyright © 2002 by Roland Stull.

.

Figure 6

Fig 6. Thermo diagram with isobars (horizontal lines labeled with P at the left), isotherms (vertical lines labeled with T at the bottom), isohumes (thin dotted lines labeled with r or rs at the top), and dry adiabats (thick diagonal lines labeled with T at the bottom). Figure copyright © 2002 by Roland Stull.

.

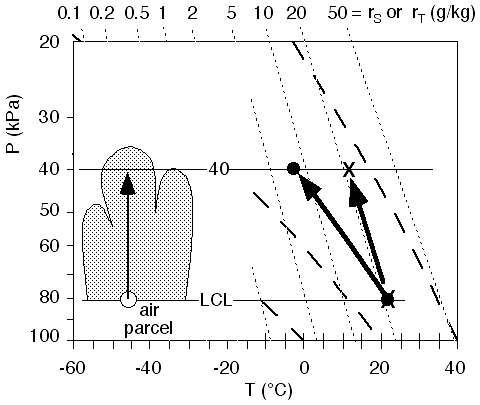
Now let's take a look at an example.

For the bottom measurement from the previous solved example (P = 100 kPa, T = 40 °C, Td = 25 °C),
1) find the pressure altitude of the LCL.
2) find the temperature, dew point, mixing ratio, saturation mixing ratio, and relative humidity at the LCL.

Answers:

The T and Td points are plotted in Fig 7 below as the dot and X, as usual. The dot is lifted along or parallel to the adiabats. The X is lifted along or parallel to the isohumes. Where those two points cross is the LCL.

Figure 7

Fig 7. An air parcel at the surface, represented by the dot for T and the 'X' for Td, is lifted to its lifting condensation level (LCL). Figure copyright © 2002 by Roland Stull.

.

1) Based on this diagram, it looks like the LCL is near P = 82 kPa. That was the pressure altitude that was asked for.

2) If I were to have plotted this on Fig 6, I would have found roughly that T = Td = 22°C, and r = rs = 21 g/kg, and thus RH% = 100% = 100 • 21/21. Thus, the state of the air at the LCL in this example is (P = 82 kPa, T = 22°C, r = 21 g/kg, and the air is just saturated).

.

c. Rise of Saturated Air Parcels

Once a rising air parcel has reached the LCL, any further rise will cause some of the water vapour to condense out into cloud droplets (which can combine into larger rain drops).

Latent heat is released during condensation. Thus, a rising saturated air parcel doesn't cool as fast as an unsaturated one. Hence, the saturated adiabats should not slope as much as the dry ones, as was already discussed in the "Storm Energy" course notes regarding the saturated-adiabatic lapse rate.

Although water vapour is condensing into liquid droplets, one assumption that can be made is that all of the liquid water, as well as remaining vapour, are still carried along with the air parcel. This is a good assumption for cloud droplets, which are so small and light that they are easily carried along with the air. What this means is that total water mixing ratio (rT) is conserved. But total water mixing ratio is defined as the sum of water-vapour mixing ratio (rs) plus liquid-water mixing ratio (rL):

rT = rs + rL

No water vapour molecules are created or destroyed during condensation; they all are conserved in one form (vapour) or another (liquid). So a simple rule is that if no liquid water has fallen out of the air parcel, then its total water mixing ratio equals its initial mixing ratio before it even started to rise from the ground (rT = rinitially).

A simplified thermo diagram with only saturated adiabats (curved, thick, dashed diagonal lines) and isohumes (thin dotted lines) is shown in Fig 8. Starting where we left off, with an air parcel at the LCL, the dot and X coincide at the LCL. But as we lift the parcel further, the X continues following the isohume, and now represents total water. The dot follows a saturated adiabat. For example, if we were to lift the parcel to a height where P = 40 kPa, then the dot and X would both be moved to this altitude, but the dot would still be on its saturated adiabat, while the X would still be on the isohume.

The amount of water vapour (r = rs) that can be held in the parcel depends on its temperature and pressure, and can be read off of the thermo diagram from the isohume that crosses through the dot. If the dot falls between two isohumes, then interpolate as best you can. Thus, knowing rT from the isohume that passes through the X, and knowing rs from the isohume that passes through the dot, we can subtract the latter from the former to find how much liquid water is being carried by the air parcel: rL = rT - rs

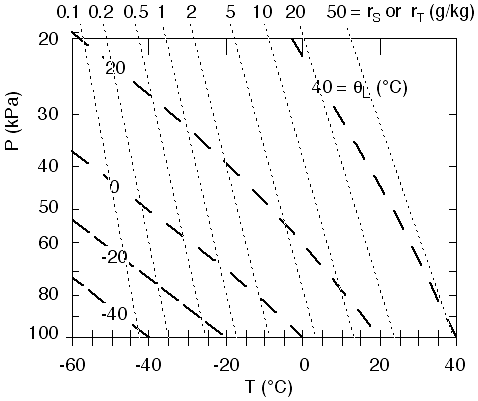
Figure 8

Fig 8. Simplified thermo diagram, showing only isohumes (thin dotted lines, labeled as r at the top) and saturated adiabats (thick dashed lines, labeled as liquid water potential temperature 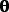L). Figure copyright © 2002 by Roland Stull.

Here's a sample question.

Starting from the LCL of the previous example (T = Td = 22°C, and r = rs = 21 g/kg, at P = 82 kPa), continue lifting the cloudy air parcel up to an altitude where P = 40 kPa. Find its temperature, saturation mixing ratio, total water mixing ratio, and amount of liquid water being carried along.

Answers:

1, 2) Moving the dot (representing temperature) parallel to the saturated adiabats, starting from the LCL, and ending at P = 40 kPa, gives: T = -3°C, and rs = 8 g/kg (see Fig 9).

3, 4, 5) For standard air, Td = T = -3°C, and r = rs = 8 g/kg. Also, moving the X (representing total water) up to P = 40 kPa still gives rT = 21 g/kg (no change).

6) Then, subtracting rs from rT gives rL = 13 g/kg. This means that each kilogram of air holds 13 grams of liquid water (cloud) droplets.

Figure 9

Fig 9. Rise of a saturated (cloudy) air parcel from cloud base to a pressure height of P = 40 kPa. The dot follow the saturated adiabats, and shows how parcel temperature changes, and the X follows an isohume, and shows total water mixing ratio. Figure copyright © 2002 by Roland Stull.

.

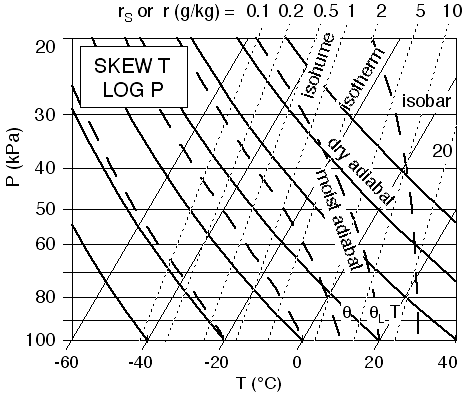
d. Full Thermo Diagram

Fig 10 shows a complete thermo diagram, which contains all of the different types of isopleths (lines of equal value) that are usually found in thermo diagrams. It contains isobars (horizontal thin solid), isotherms (vertical thin solid), isohumes (nearly vertical thin dotted), dry adiabats (diagonal thick solid) and saturated adiabats (curved thick dashed). The isobars, isotherms, and isohumes are labeled at the left, bottom, and top, respectively. The dry and saturated adiabats are labeled at the bottom, by the temperatures where they cross the 100 kPa isobar.

Figure 10

Fig 10. Complete thermo diagram. Figure copyright © 2002 by Roland Stull.

.

1) Printout S3 shows a full-size thermo diagram. It contains exactly the same information as Fig 10, but is larger and more detailed. This allows you to compute your answers a bit more accurately, because interpolation is easier. This type of thermo diagram is called an emagram. Click here to open Printout S3.

2) There are other types of thermo diagrams that are used, and which can be viewed on various web pages. These include the tephigram, Skew-T Log P (known as Skew-T for short), Stuve, and pseudoadiabatic diagrams. The Stuve and pseudoadiabatic diagrams look very similar to the emagram that was explained here. So these should be relatively easy for you to use too.

a) The tephigram and skew-T look similar to each other, but not to the emagram. An example of a skew-T is shown in Fig 11. The main difference is that the isotherms are not vertical, but they tilt upward to the right. The isohumes and adiabats are also rotated slight to the right. Whenever you encounter a new thermo diagram, take some time to read the legend and labels to figure out where the isobars, isotherms, isohumes, and dry and saturated adiabats are.
.
b) For example, plot the sounding from Table 1 on this Skew-T diagram (answer not shown here). Once you have done that, you can use the diagram analogously to what has been described in all the previous examples.

Figure 11

Fig 11. Skew-T Thermo Diagram. Figure copyright © 2002 by Roland Stull.

.

4. Static Stability

a. Buoyant Forces

If an air parcel is warmer than its environment, buoyancy tries to make it rise (or slows its descent if previously sinking). If the air parcel is colder than the environment, buoyancy tries to make it sink (or slows its ascent if previously rising). If the parcel and environment are the same temperature, then there is no net buoyancy force; therefore the parcel stays put if previously not moving, or continues to coast if previously moving.

b. Stability Classes

Air is said to be statically unstable if the buoyancy force is in the same direction as the current movement of the air parcel. Unstable air tends to become very turbulent with strong vertical motions, and supports cumulus clouds and thunderstorms.

Air is statically stable if the force opposes the current movement. Stable air has minimal vertical motions, and is often nonturbulent (smooth or laminar), can support smooth vertical oscillations (waves) in the air, and supports stratiform clouds.

Air is statically neutral if there is no buoyancy force. Neutral layers are often created by strong turbulent mixing. So even though they don't enhance or surpress their own turbulence, we must take care to see if factors from outside are creating turbulence.

Air is conditionally unstable if it opposes vertical motion for unsaturated air, but enhances vertical motion for saturated (cloudy) air. Hence, different air parcels behave differently within this layer, depending on whether the parcel is cloudy or not.

That's all there is to static stability. Sounds easy enough.

But there are two tricky aspects.

  1. When an air parcel moves up or down, its own temperature changes according to the dry or moist adiabatic lapse rate (when it is unsaturated or cloudy, respectively).
  2. As the air parcel moves up or down, it moves into different layers of the atmosphere that have different environmental temperatures.

Thus, you must take care when moving air parcels up and down to see how both the parcel and environmental conditions are changing, in order to determine the forces that might cause continued or future movement.

Thermo diagrams were designed to make this job easier, as will be utilized in the following subsections.

c. How to Determine Layer Stability

There are two ways to identify stability. One is layer stability, and the other is parcel stability. Parcel stability will be discussed in section 5, and is used for estimating thunderstorm intensity. Layer stability just looks at the environment, as will be summarized in this section.

For illustration of layer stability, lets start with the sounding from the previous solved example.

P (kPa)
T (°C)
Td (°C)
20
-30
-60
30
-30
-45
50
-10
-35
65
10
-20
80
25
-5
90
25
20
100
40
25

Table 1. (again) Atmospheric sounding of the environment.

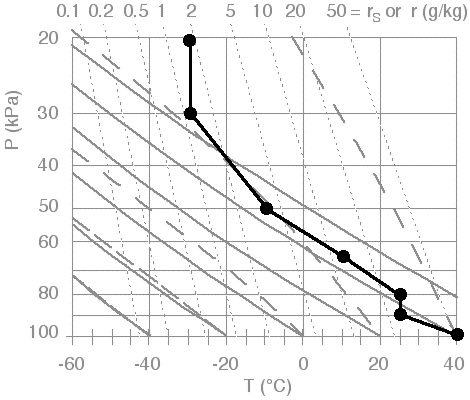
I will start with the blank thermo diagram of Fig 10, and plot just the temperature part of the sounding to produce the result shown in Fig 12. You should follow along, but using Printout S3 instead.

Figure 12

Fig 12. Plot of environmental sounding (temperature part only). Figure copyright © 2002 by Roland Stull.

.

1) We will look at unsaturated (non-cloudy) layer stability. First, determine unstable regions. For each data point that was plotted, conceptually raise it a little bit as if it were an air parcel, but do this following (or parallel to) a dry adiabat. If this parcel is warmer than its surroundings at the same altitude, then continue to lift it following the dry adiabat until it crosses the sounding again. The region between the starting point and where it crosses the sounding is labeled as "unstable". Do this for all the other starting points (original data points), to identify all the unstable regions.

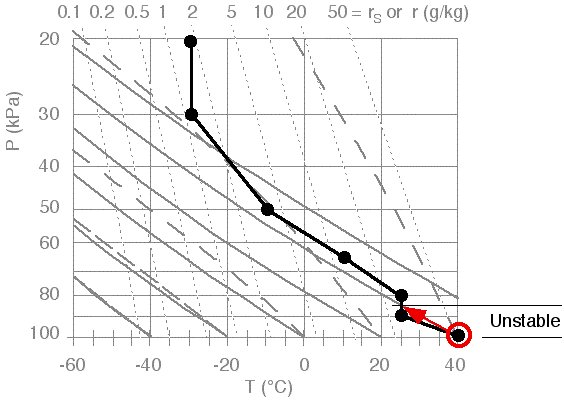
In the illustration of Fig 12, we find that the data point at the ground (starting at P = 100 kPa) is unstable if lifted. Because it is warmer than its surrounding environment, it would continue to rise along a dry adiabat until it hits the sounding (at about P = 85 kPa for this sounding). Notice that the top of this unstable layer doesn't have to be at another data point; namely, it can be inbetween two data points if that is where the rising parcel happens to cross the sounding. The result is shown in Fig 13. When we conceptually start lifting the other data points in this sounding, we find no other unstable layers. So for this particular example, there was only one unstable layer, as is plotted in Fig 13.

Figure 13

Fig 13. Unstable layers identified by conceptually lifting data points along dry adiabats. Figure copyright © 2002 by Roland Stull.

.

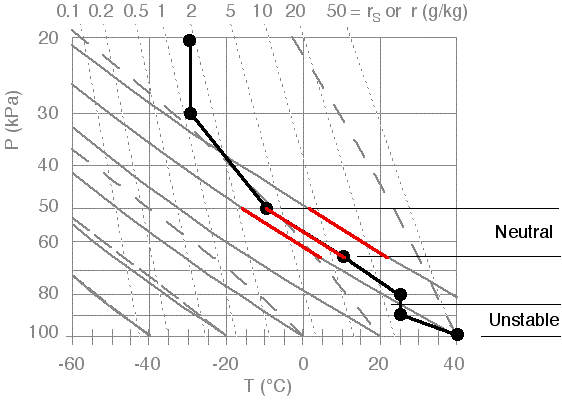
2) Next, identify statically neutral layers. Do this only for those regions NOT already identified as unstable. Neutral regions are where the sounding is nearly parallel to the nearest dry adiabats. These are identified in Fig 14. In this illustration, there is only one neutral layer. Note that there is another layer just below 65 kPa that is nearly neutral (i.e., nearly parallel to the dry adiabats), but not quite. This layer is so close to neutral that it would have been acceptable to also identify it as neutral.

Figure 14

Fig 14. Illustration of identifying statically neutral layers. Figure copyright © 2002 by Roland Stull.

.

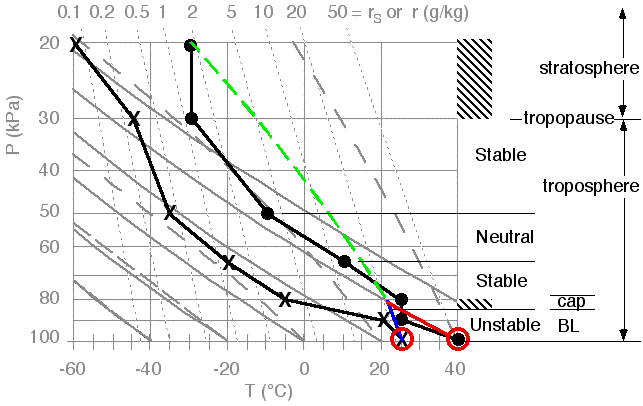
3) Finally, identify the stable layers as any remaining layer. Stable layers are said to be strongly stable if T is constant with height (isothermal), or if T increases with height (temperature inversion). This is done in Fig 15, which now holds the complete stability classification of all the regions in the sounding.

4) In this illustration, two of the stable layers are isothermal (one between P = 20 and 30 kPa, and the other between 80 and 85 kPa), and there are no inversion layers. I've indicated these regions of strong stability with cross hatching.

.

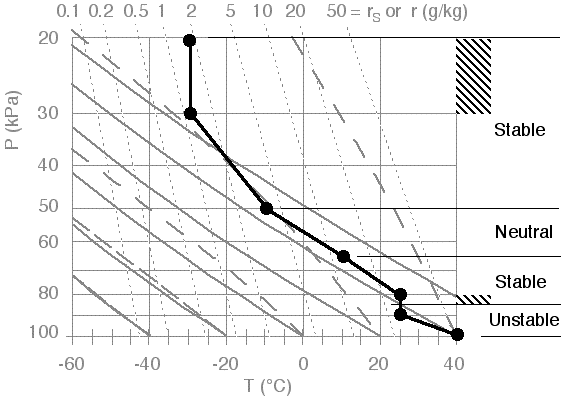Figure 15

Fig 15. Stability of the whole sounding, where regions of strong stability are identified with cross hatching. Figure copyright © 2002 by Roland Stull.

.

Different layers of the atmosphere have different stabilities. For example, the stratosphere is always strongly statically stable. Namely, vertical motions are opposed because the stratospheric environment is isothermal (T constant with z) in the bottom 1/4, and has a deep temperature inversion (T increases with z) in the top 3/4. Thus, the base of the stratosphere (averaging 11 km altitude) always acts like a lid or cap to ALL weather in the troposphere, including thunderstorms, hurricanes, and cyclones.

Below the stratosphere is the troposphere (0 - 11 km), where most of our interesting weather happens. The dividing line between the troposphere and stratosphere is called the tropopause, or "trope" for short. Within the troposphere, stabilities vary from place to place, season to season, day to day, and hour to hour. So we must frequently measure the environmental sounding and air-parcel conditions to see how the static stability is changing. Most national weather services around the world make routine upper-air soundings twice a day or more frequently, in order to monitor such instabilities.

d. Interpretation of the Results

Now that the stability of the whole sounding has been identified in Fig 15, we can identify it as the thunderstorm environment. This interpretation is written in Fig 16, where we have also plotted the dew point temperatures that we have ignored so far.

1) "BL" is the boundary layer, holding the warm, humid air that is fuel for the storm. A deeper, warmer, and more humid BL could support more thunderstorm activity.

"Cap" is the capping stable layer, which is both good and bad for the thunderstorm. It is good because it traps the warm, humid air below it in the boundary layer, to serve as a reservoir of fuel for the thunderstorms. But this cap must first be broken by some outside trigger, in order to get the fuel up to where condensation can release its latent heat to power the thunderstorm. A thicker and more stable cap inhibits convection and is more difficult to break, making thunderstorms less likely to start.

2) The stratosphere is the isothermal layer near the top of the sounding. The tropopause at the base of the stratosphere marks where the top of the thunderstorm will be. The anvil cloud can be expected to spread out just under the tropopause.

The rest of the troposphere, above the cap and below the tropopause, is where the active part of the storm can be. There is where latent heat is released through condensation, and where the resulting extra buoyancy drives the vertical circulation that continues to draw in more boundary layer fuel. Thunderstorm severity (hail, downpours, downbursts, turbulence) increases if this middle layer is drier and colder.

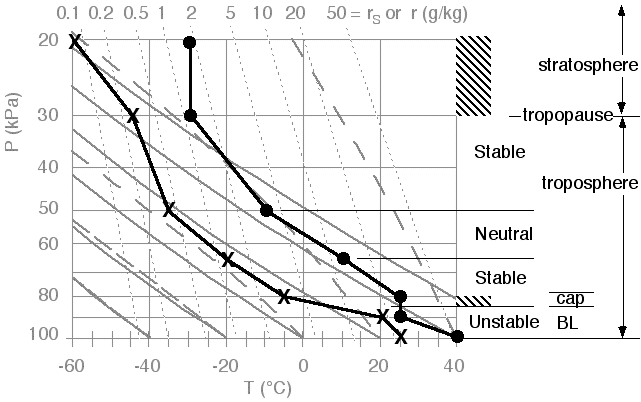Figure 16

Fig 16. Interpretation of the environmental sounding. Figure copyright © 2002 by Roland Stull.

.

3) The conditions that are most conducive to severe thunderstorms are warm moist air near the ground, capped by a statically stable layer, with dry air in the mid troposphere and cold air aloft.  This arrangement creates a conditionally unstable atmosphere. We haven't talked about wind yet, but when rawinsonde balloons are launched to measure the upper air sounding, they also report back winds at each height. The change of wind speed or direction with height is called wind shear. Wind shear near the ground is good for the thunderstorm, because it helps advect the warm humid boundary layer air that fuels the storm, allowing the storm to be longer lasting. The shear also creates a twisting motion (vorticity) that can be tilted into a tornado by the thunderstorm. Strong winds aloft also favor intense, rotating, long-lived thunderstorms called supercell storms.

.

5. Predicting Storm Intensity

a. How to Find Parcel Stability

The next step in estimating likely thunderstorm intensity is to see what would happen if a warm, humid air parcel were forceably lifted from near the surface by a trigger mechanism. Such parcel stability must consider that an air parcel from the surface can pass through many layers; hence, we must look beyond simple layer stability.

By combining information on air parcel behavior (section 3) with information on the environment (sections 2 and 4), we can estimate both trigger strength needed to kick start the storm, and intensity of the resulting storm.

The steps to do this are:

(a) Plot and interpret the sounding on a full thermo diagram (as was shown in section 4).
(b) Track an air parcel lifted from the surface to the top of the sounding.
(c) Determine lifting or heating needed by a trigger to break the inversion.
(d) Find the depth and energy of the storm.

We have already illustrated step (a) in the previous section.

b. Tracking Parcel Rise

We will conceptually lift an air parcel from the surface up to the top of the sounding, regardless of whether the parcel is buoyant or not. Along the way, it will pass through many layers. For now, assume that the starting T and Td of the air parcel are assumed to be the same as those measured at the very bottom of the environmental sounding (i.e., the bottom data point).

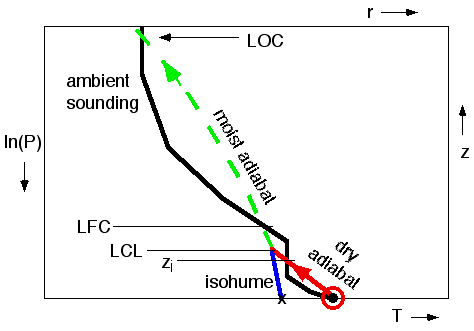
As we learned in section 2, start by moving the temperature along (or parallel to) a dry adiabat (shown in red in Fig 18), and moving the dew point along (or parallel to) an isohume (shown in blue), until they meet at the LCL. Above the LCL, have T follow (go parallel to) a saturated adiabat (shown in green) up to the top of the sounding. For now, ignore (don't plot) Td and rT above the LCL.

Figure 18

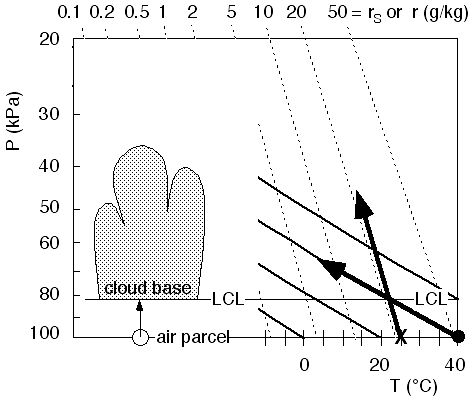
Fig 18. Tracking the rise of an air parcel from the surface. Figure copyright © 2002 by Roland Stull.

.

Interpreting this figure, we see that the surface air parcel could rise due to its own buoyancy through the boundary layer, and up to the capping stable layer at pressure altitude 85 kPa. The symbol zi is used to designate the top of the boundary layer.

To go higher, it would have to be forceably lifted through this cap, because the parcel at these altitudes is cooler than the environmental sounding, and would prefer to sink rather than rise because of its negative buoyancy. However, if such lifting did occur, the parcel would reach its Lifting Condensation Level (LCL), which marks cloud base.

If the (now cloudy) parcel were forceably lifted high enough, it would find itself warmer than the environment again. This altitude is called the Level of Free Convection (LFC). Above the LFC, the parcel could continue rising on its own buoyancy up until it hits the the sounding again in the lower stratosphere. This top altitude is called the Limit of Convection (LOC), and marks cloud top.

These various altitudes are sketched in Fig 19, which is a simplified version of a thermo diagram.

Figure 19

Fig 19. Key altitudes for parcel stability, sketched on a bare-bones thermo diagram. Base and top of the thunderstorm cloud are at LCL and LOC, respectively. Figure copyright © 2002 by Roland Stull.

.

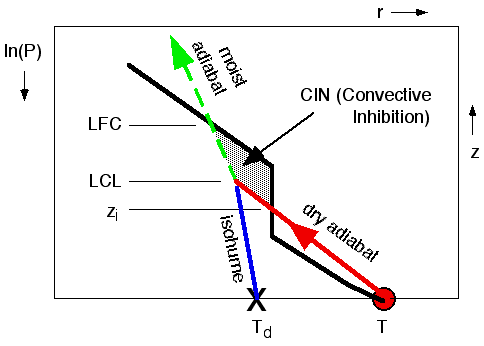
c. Convective Inhibition (CIN) and Triggering

In the previous subsection, we saw that the region between the top of the mixed layer zi and the LFC is the region where the air parcel is cooler than the surrounding environment. This is the region that inhibits convection; namely, it acts like a lid to updrafts, preventing them from vertically growing into thunderstorms. It is the region that must be overpowered by forced lifting by an external trigger mechanism, or eliminated via more heating from the surface.

The strength of this lid is measured by the area between the ambient sounding and the air parcel temperature (shaded in Fig 20), for only the portion of the air parcel temperature that is cooler than the environment. This area is called the Convective Inhibition (CIN). Larger values of CIN correspond to stronger lids, and indicate that triggering of thunderstorms is more difficult (i.e., a stronger trigger is needed to kick start a thunderstorm). Smaller CINs indicate that thunderstorms are more easily triggered, and thus more likely (everything else being equal).

Figure 20

Fig 20. Enlargement of the bottom third of Fig 19. Black line represents the ambient environmental sounding. Red circle represents an air parcel starting near the surface. Red and green lines show how the air parcel temperature changes as it rises. Convective inhibition (CIN) is the area (shaded) between the top of the mixed layer zi and the level of free convection LFC. Figure copyright © 2002 by Roland Stull.

.

Two ways of eliminating the effect of this lid are by forced lifting, or by heating of surface-layer air. The first method overpowers the lid, the second eliminates the lid.

1) Forced lifting could be caused by a cold front, gust front, dry line, or sea-breeze. In these situations, an advancing wedge of cold air drives under the warm air parcel and forces it upwards. This is because the advancing cold air is heavier than the warm air parcel, and tends to ride under the parcel. This way, the air parcel can be forced up to its LFC, even though the parcel buoyancy is negative during a portion of its rise. A similar trigger mechanism is where the wind blows the warm air parcel to a mountain slope, forcing the parcel to rise upslope. A thunderstorm triggered this way is called an orographic thunderstorm. These forcings are illustrated in Fig 21. For Fig 18, the LFC is of approximately 73 kPa. A better estimate is possible using the full thermo diagram of printout S3.

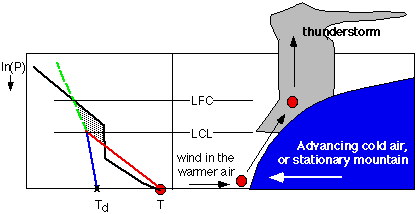Figure 21

Fig 21. Air parcel (red circle) being forced upward over an obstacle. The obstacle could be a mountain, or a mass of cold air advancing as a cold front or as a gust front from a different, older thunderstorm. If forced up past the LFC, then the parcel can continue rising by its own buoyancy, to create a thunderstorm. Figure copyright © 2002 by Roland Stull.

.

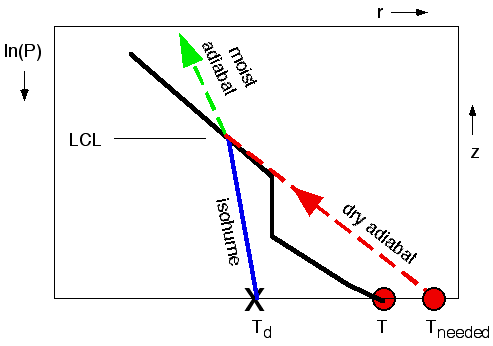
2) Thunderstorm convection can be initiated due to surface heating that eliminates the lid, as sketched in Fig 22 for the bottom third of the troposphere again. The black line might represent the environmental sounding in mid morning, where part of the isothermal layer caps thermals rising from the surface. We can anticipate that if the surface temperature becomes warm enough (Tneeded in Fig 22), then the air parcel would always remain warmer than the environment sounding as it rises. This critical temperature is called the convective initiation temperature. If more and more heating from the sun during the day causes the near-surface air temperature to warm toward this critical temperature, then we could forecast thunderstorms to begin when that critical temperature is reached.

From Fig 18, Tneeded = 45°C, approximately. A better estimate of Tneeded can be found using the full thermo diagram in prinout S3.

Figure 22

Fig 22. The lid can be "burned off" if the surface air temperature warms sufficiently (from T to Tneeded) during the day so that the adiabatic rise of the surface air parcel (dry adiabatically up to its LCL, and moist adiabatically above that) is everywhere warmer than the ambient environment sounding. Figure copyright © 2002 by Roland Stull.

.

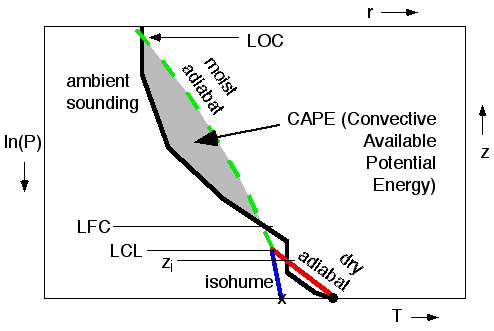
d. Convective Available Potential Energy (CAPE)

Once a thunderstorm is successfully triggered, the next question is "how intense could it become?" One indicator is the depth of the storm: deeper storms are generally more violent. The top of the thunderstorm is near the LOC, and the base is near the LCL. The difference between these two heights is the depth of the storm. Thus, thunderstorms with tops in the lower stratosphere and bases near the ground are often severe.

A more quantitative way to estimate storm intensity is by the area (shaded in Fig 23) between the air parcel's moist adiabat and the environmental sounding (above the LFC and below the LOC). This area is proportional to the Convective Available Potential Energy, or CAPE for short. Larger CAPE areas indicate more intense storms. The reason is that buoyant forces are proportional to how much hotter the rising air parcel is compared to the environment. The acceleration of this air parcel also depends on the vertical distance over which this positive buoyancy acts. The combination of this vertical distance times temperature excess is the CAPE area just described.

The relationship between CAPE and potential storm intensity is given in Table BB, where CAPE(m2/s2) = 38 • CAPE (°C • km).

.

Table BB. Estimates of thunderstorm intensity vs. CAPE.

CAPE (°C • km)
CAPE (m2/s2)
Intensity
CAPE < 0
CAPE < 0
No convection
0 < CAPE < 26
0 < CAPE < 1000
Weak convection / cumulus
26 < CAPE < 66
1000 < CAPE < 2500
Moderate thunderstorms
66 < CAPE < 92
2500 < CAPE < 3500
Strong thunderstorms
92 < CAPE
3500 < CAPE
Severe thunderstorms

.

Figure 23

Fig 23. CAPE indicates the possible intensity of the thunderstorm, and is proportional to the area shaded. In this region, the air parcel is warmer than the environment, and tends to accelerate upward due to its positive buoyancy. Figure copyright © 2002 by Roland Stull.

.

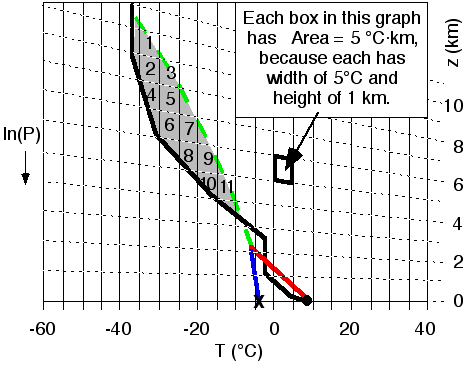
To estimate the CAPE area, a quick way is to count the number of boxes of T (°C) vs. z (km) needed to fill the shaded area. Multiply this number by the area of each box, to get the total area in units of °C·km.

To do this, we can use a version of the thermo diagram that also has lines of constant height (z) plotted. These lines are called heights or contours, and are shown in Fig 24. Also, the full-size thermo diagram of Printout S3 has the height contours. It is this full size diagram that should be used for all real soundings, because it is more precise.

In Fig 24, we have numbered each box that is filled with shading just to illustrate the box counting. If some boxes that we counted are only partly shaded, then we must compensate by not counting other partially shaded boxes. Use your judgement, so that the total area tiled by these boxes is roughly equal to the total area shaded in the CAPE diagram. For example, box 1 is not fully shaded -- the upper right corner is missing shading. However, there is a little bit of extra shading in the box just left of box 1, and an even smaller bit in the box above that. By eye, the portion of shading in these additional boxes looks about right to compensate for the empty corner of box 1. Similar judgement calls must be made for the other boxes.

For Figs 23 and 24, I count 11 boxes. In this diagram, each box is 5°C wide by 1 km high; thus, each box has an area = (5°C)·(1 km) = 5 °C·km. Thus, the total area = (11 boxes) x (5 °C·km/box) = 55 °C·km. However, the diagrams in Figs 23 and 24 were meant for illustration only. The sounding plotted in them was not the same as the sounding of our example that we have been using through-out this lab.

Figure 24

Fig 24. Method of calculating CAPE, by counting the number of boxes needed to fill the shaded area. The dotted, nearly horizontal lines are height contours, labeled by z on the right. Figure copyright © 2002 by Roland Stull.

.

For figures 23 and 24, CAPE = 55 °C•km for which Table BB indicates moderately intense storms.

Let's see an example.

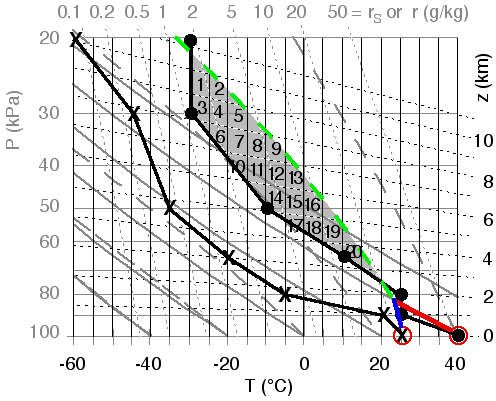
Given Fig 25, which shows the original sounding plotted on a thermo diagram that has the extra height lines and temperature lines to calculate CAPE.

1) In Fig 25, draw lines for the rise of the surface air parcel following dry or moist adiabats as appropriate, up to the top of the diagram. The LOC of the top of the storm is approximately at p = 22kPa.
2a) Identify the CAPE area, count the boxes in it.
2b) Determine the total area tiled by the boxes. This area is the CAPE = ____________°C•km
2c) Classify the intensity of the thunderstorm.
Figure 25

Fig 25. The original sounding of Table 1, plotted on a complete thermo diagram with height (z) and temperature (T) lines highlighted. The red circles indicate the temperature and dew-point of the surface air parcel. Figure copyright © 2002 by Roland Stull.

Answers:

The answer is shown in Fig 26, with red lines showing the dry adiatabic rise of the parcel up to its LCL, and the green line showing the remainder of its rise parallel to the moist adiabats. The CAPE area between the parcel and the environment, above the LFC and below the LOC is shaded. I count roughly 20 boxes, where each box in this diagram area = 5 °C·km. Thus, I get a total convective available potential energy of CAPE = 20 • (5 °C·km) = 100 °C•km, which suggests that severe thunderstorms are possible.

Figure 26

Fig 26. Rise of the surface air parcel (red circle) is shown with the red, blue, and green lines. CAPE is proportional to the shaded area between the moist adiabat (green line) of the rising air parcel, and the temperature (black line) of the environment. This area can be covered by roughly 20 boxes, where each box is 5°C wide and 1 km high. Figure copyright © 2002 by Roland Stull.

.

6. Final Conclusions and Review

Copyright 2002 by Roland Stull
UBC ATSC
.