| |
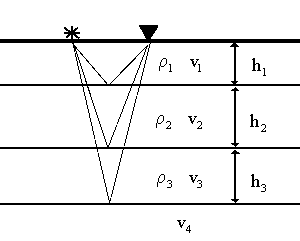
The principles of the normal incidence reflection seismogram are illustrated
in the diagrams below. A source and receiver are at the surface of a layered
earth whose properties are variable. The reflection and transmission coefficients
depend upon the change in acoustic impedance, and thus on both density
and velocity. The travel time for the wave to go from the source to the
reflecting interface and back to the surface depends only upon the length
of the travel path and the velocity of each layer. The travel time formula
given below, is for a wave which travels vertically and for which the source
and receiver are coincident. (The source and receiver are offset slightly
in the diagram for visual clarity). This produces the "normal incidence" seismogram.
 |
Acoustic Impedance: |
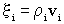 |
If amplitude of incident is Ain and
amplitude of reflection is
Aref than the reflection coefficient ri gives Aref/Ain (ratio
of reflected to incoming amplitudes).
Ratio of energy in to reflected
energy is ri2. |
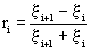 |
| Incremental travel time (vertical
travelling wave): |
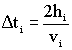 |
The normal incidence seismic trace is obtained by the convolution of
a seismic wavelet (input pulse) with the reflectivity function. The amplitude
of each spike on the reflectivity function is equal to the value of the
reflection coefficient that corresponds to a particular boundary. (In reality
this value is further altered by the transmission coefficients). The times
for each reflection event are obtained by knowing the layer thickness and
velocities. Each impulse on the reflection function generates a scaled
replication of the seismic wavelet. The composite of all of the reflection
events generates the seismic trace.
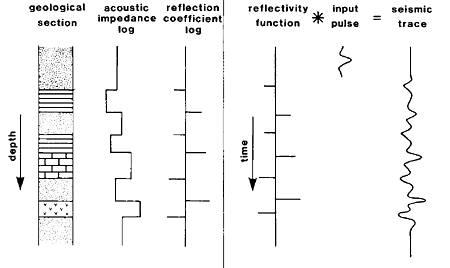 |
The reflection seismogram viewed as the convolved output
of a reflectivity function with an input pulse.
From Kearey, Philip and Micheal Brooks, An Introduction to Geophysical
Exploration. 2nd ed. Blackwell Science: 1991. |
Notice how the negative reflection coefficients chage the polarity of
the signal recoreded at the receiver.
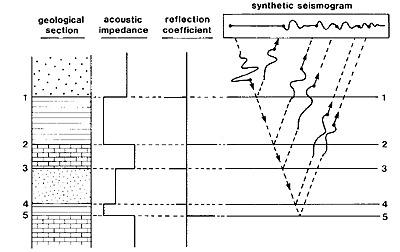 |
A synthetic seismogram.
From Kearey, Philip and Micheal Brooks, An Introduction to Geophysical
Exploration. 2nd ed. Blackwell Science: 1991. |
|
|

