aglo

Refraction Interpretation for Horizontal Layers
 

The goal of a seismic refraction experiment is generally to determine depth to bedrock, depth to water table, or to delineate major sedimentary layers. In its complete generality, the seismic refraction problem is quite complicated. However, there are certain geometries for which formulae can be generated to predict the arrival times. With the aid of these formulae, measurements of the refracted arrivals can be used to determine layer parameters. We will restrict ourselves to the following situations:

  1. The subsurface is composed of layers separated by planes and possibly dipping interfaces.
  2. The seismic velocity in each layer is constant.
  3. The layer velocities increase with depth.
  4. The ray paths are in the vertical plane. That is, there is no cross-dip (which means dipping into or out of the page in the figure to the right). 

With the above assumptions, there are a number of special cases to be considered.

  1. A 2-layer earth with a horizontal interface.
  2. A 3-layer (and multiple-layer) earth with horizontal interfaces.
  3. A 2-layer earth with a dipping interface.

In all cases, the development of the travel-time curves requires only that we know the rules of propagation, i.e., energy travels in straight lines in a uniform medium and refracts according to Snell's law when it enters a medium with different velocity. We must also be able to calculate the lengths of the ray path in each layer and along the refractor. Travel-time curves are graphs showing the travel-time, t, (length of time for a seismic signal to travel from the source to the receiver along which ever path is being considered) versus distance between the source and receiver, x.

One layer over basement - the horizontal interface

 

We want relations involving things we want in terms of things we either know of can get. We want depths, but in fact, we can get travel times in terms of distances (known) and velocities (obtainable - see below). Depth is obtained as a last step.

Consider an earth composed of a uniform layer with velocity V1 and thickness z overlying a medium with velocity V2. Let [theta] be the critical angle and x denoted the distance between the source at A and a receiver at D.  Let xc denote the critical distance.

 

From elementary geometry the following relationships hold: 
, 
or 

The travel time is the cumulative time for the wave to traverse the path ABCD. This is t=tAB+tBC+tCD.

Generally time = distance / velocity, so we can write tAB = L/v1 = (z/cos([theta])) / v1, (using L from just above).

Also, we can note that tAB = tCD and the distance BC is X-XC. So we can now state that t=2tAB+tBC , or

.

It is convenient to rearrange this slightly differently. Using the definition for critical angle  sin[theta]=V1/V2, we can make the "velocity triangle", so expressions for the angle arise directly from simple trigonometry:

Use these two relations for cos and tan in the expression for t above to obtain a useful set of relations.

You can convince yourself that x is in fact the complete distance between shot and geophone by carrying out the intermediate analysis steps.

This simple relation says that the travel time curve is a straight line which has a slope of 1/V2 and an intercept of ti. This intercept time is the time where the refraction line extends to intercept the Y-axis above the source position. This is not a real "time" - it is derived from the graph.

The velocities of the seismic layers and the layer thickness are obtained in the following manner. 

  1. Plot the times of first arrivals on an time-offset plot ("offset" is distance between source and geophone).
  2. The direct arrivals are observed to lie along a straight line joining the origin. The slope of this line is 1/V1, giving the velocity of the upper layer.
  3. The refracted arrivals appear as a straight line with smaller slope equal to 1/V2, giving the velocity of the lower layer. 
  4. For the refracted wave, this intercept time is 

We therefore can obtain all three useful parameters about the earth, (V1, z, V2).

There is another useful point that is observable from the first arrival travel-time plot. We can often discern the crossover distance. Since this is the location where the direct wave and the refracted wave arrive at the same time, we can write


Thus 
Combine to obtain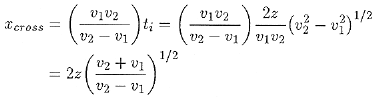 

This can be used as a consistency check, or it can be used to compute one of the variables given values for two others.

Two Horizontal Layers Over a Halfspace

The extension to more layers is in principle straight forward. However, the algebra is slightly more involved because we need to compute the times due to the ray path segments in the two top layers. Consider the diagrams below:

[F. Jones]

Using arguments that are entirely analagous to the two layer case (above) the travel time for the wave refracted at the top of layer three is given by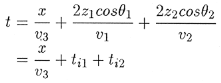

All quantities are defined in the diagrams, and the angles are
.
Note that [theta]2 is a critical angle while [theta]1 is not. You can prove the relation for [theta]1 yourself by using Snell's law at the two interfaces, and recalling that the angle of the ray coming from point B is the same as the angle arriving at point C.

The straight line that corresponds to an individual refractor provides a velocity (from its slope) and a thickness (from the intercept). Thus the information on the above travel-time plot allows us to recover all three velocities and the thickness of both layers.

The travel time curves for multi layers are obtained from obvious extension of the above formulation.