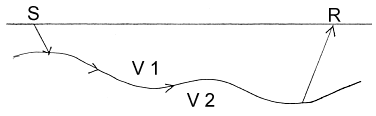
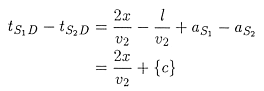There is one more step in sophistication that is required so that the refraction technique is useful. This occurs in environments where the interface has topography and is no longer approximated by a plane. If the curvature of the interface is not too great then we can still think of the refracted wave travelling along the interface. The wave travels at the speed of the lower medium. Consider the sketch to the right. Formulae which explicitly assume a plane interface (even dipping) do not work well enough. We need a better approximation. |
 |
We would like to be able to obtain the depth of the interface beneath the source and receiver. To do this we used the concept of delay time. Consider the diagram to the right. The travel time is t = x/V2 +ti where ti can be thought of as the time delay. |
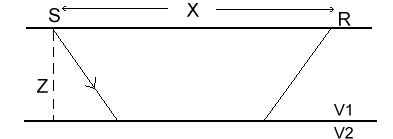 |
The delay time can be partitioned into two parts: (1) the "delay" associated with the source location and the (2) "delay" associated with the receiver location. Consider the delay at the source.
Let the delay time be denoted by 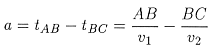 . . |
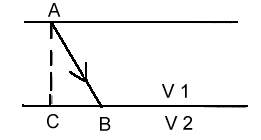 |
We need to use AB=z/cos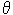 , BC=ztan , BC=ztan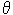 , and Snell's law (sin , and Snell's law (sin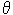 =v1/v2, or v1=v2sin =v1/v2, or v1=v2sin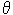 ). Then we can write the delay time as follows, where we arrive past the second equals sign by using some trigonometric identities. ). Then we can write the delay time as follows, where we arrive past the second equals sign by using some trigonometric identities.
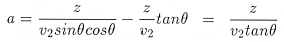 . .
Finally, using the definition of the velocity triangle we can write 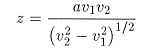 (eqn 1). (eqn 1).
Thus the depth can be computed if the delay time, a, can be measured.
We can write any general travel time so that it involves a delay at the source as and a delay at the receiver or detector ad. It looks like this: 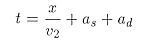 . .
As in the diagram at the top of this page, as and ad might be very different. To make progress we implement Hagedoorn's "Plus-Minus" method.
This method will also make it possible to estimate depths under every geophone that has a refracted signal from both sources. This will yield several depths under the survey line rather than just two depths under sources, thus allowing more detailed image of the interface's shape. Hagedoorn's Plus-Minus Method
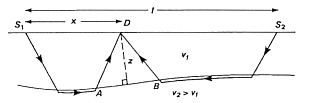
The geometry illustrates the two shots occurring at locations S1 and S2. The point indicated by D lies at any location (ie any geophone) between the two shots where refractions can be received from both shots. Let aS1 and aS2 denote the delay times at the two shot locations. Although the refracting interface is not flat beneath D, the slope is not large and the ray path lengths AD and BD are almost identical.
Let us write all portions of the travel times for signals that would travel between S1 and S2, between S1 and D, and between S2 and D. These travel times are:
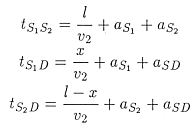 . . |
 |
The "Plus" term gives "delay time" at a geophone
When the last two equations are added together, we see that the result includes the expression for the first. Here is what we get:
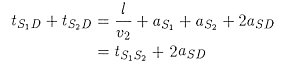 . .
Rearranging this equation gives us the so-called "Plus" result, which is in fact the delay time beneath location D. In involves travel times that are measured - namely the refracted arrival time to D from both shots 1 and 2, and the time a signal would take to travel from shot 1 to shot 2. This is the reciprocal time introduced earlier.
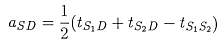 .
.
Referring back to the expression for z labelled (eqn 1) above, the depth to the refractor under position D can therefore be given by
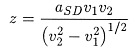 .
.
This can be evaluated if the two velocities are known.
The "Minus" term gives V2 under D.
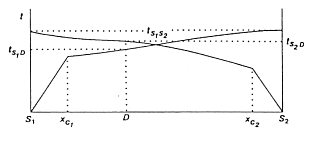
We will assume that V1 is known from the direct arrivals. It remains only to find V2. Unfortunately it cannot be obtained directly from the first arrival plot. The refractor surface is irregular and thus the travel time curve for the refractor is warped. The sketch here illustrates the difficulty. |
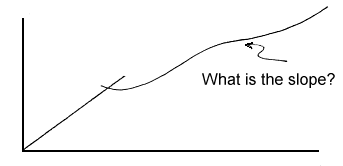 |
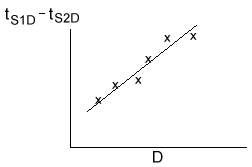
To obtain about the velocity we look at the difference in arrival time at location D. Subtracting the two equations yields
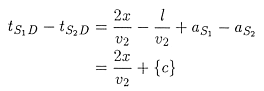 where the constant c is fixed for fixed S1, S2. This suggests that v2 will be the slope of some straight line. But what is plotted to get this slope? Not t vs X, but (tS1D- tS2D) vs X. The explanation follows:
where the constant c is fixed for fixed S1, S2. This suggests that v2 will be the slope of some straight line. But what is plotted to get this slope? Not t vs X, but (tS1D- tS2D) vs X. The explanation follows:
Suppose we have a number of receivers between locations D1 and D2. For each receiver we can measure the refracted arrivals from both shots. The time  t = ts1D - ts2D can be computed for each detector and plotted on a graph. According to the equation above, the slope of this graph should be 2/V2. From the above analysis we can obtain an estimate of the depth of the refractor and the velocity of the refractor. t = ts1D - ts2D can be computed for each detector and plotted on a graph. According to the equation above, the slope of this graph should be 2/V2. From the above analysis we can obtain an estimate of the depth of the refractor and the velocity of the refractor.
Note that this "Plus-Minus" method works well if the dips are small (< ~10o ), but begins to be less successful for steeply dipping interfaces. |
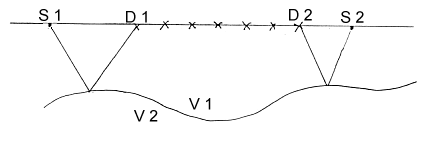
|
|


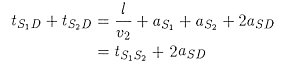 .
.
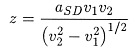 .
.