Inversion concepts:  
The inversion process

Objectives

This page outlines how inversion works without going into details. After absorbing the concepts, you should be able to:

1. Explain the difference between observed and predicted data;
2. Understand why both are needed;
3. Give three reasons why we say that the inversion problem is "non-unique";
4. Understand that there will still be significant "prior knowledge," even though geophysical work may be done at a site where very little previous work was done. 
5. Have a preliminary appreciation for various ways of examining 3D models that are built using a discrete set of rectangular cells.

Introduction

In this section we step through the major ideas involved in carrying out practical inversions and we develop a generic flow chart for the process that will be used throughout this CD. The two types of constraints on the model - data and prior knowledge - will be emphasized. We must understand how they can be used to decide whether the computed model is a good candidate for the earth structure. We also talk about the importance of visualizing and presenting resulting models in a meaningful way. Finally, we sum up with a new, more complete flow chart, which will serve as the basis for discussions about inversion throughout the CD-ROM.

Inversion and forward modelling

To reiterate, the goal of the inversion is to produce a reasonable model that generated data, given field survey observations, some knowledge about their errors, a decision about how to represent the earth and an ability to forward model. Also, the distinction between forward modeling and inversion must be clear, as summarized in the following interactive figure.

1a. Calculating data when the model of the Earth is known is called forward modeling. 1b. Iinversion is the opposite procedure - estimating possible models when data are available. 1c. For most problems the earth will be represented with discrete rectangular cells.

Getting the process started

Unlike other geophysical "data processing" procedures such as filtering or data reduction, inversion does not take a raw data set, manipulate it directly and output some sort of answer. That is why the flow chart is not a simple linear path with data at one end and resulting model at the other. Instead, inversion processing starts with an initial estimate for the earth model, then proceeds with a forward calculation on that model to predict what measurements would be if a survey were carried out over that initial model. The resulting data set is called the predicted data. Only at this stage is the actual field data, or "observed data," brought in. These survey results are compared to predictions generated for the initial model. This is the first of two decisions in the inversion algorithm, and both are described in more detail next.

Decision number 1: Fitting the data

Once there is a preliminary model, a predicted data set for that model, and an observed data set collected in the field, the inversion algorithm can go to work on the two decisions that have to be made within the inversion process. (The important business of how to estimate a model will be discussed in detail in a subsequent chapter). The decisions are not necessarily made "first" and "second", but we will start by outlining the misfit decision using the following figure:

2a. Once a model has been estimated (initially it could be as simple as a halfspace) ...
2b. ... a data set must be calculated by forward modelling. This data set is referred to as predicted data.
2c. Data from field surveys are now brought in, ...
2d. ... and compared to the calculated data obtained by forward modelling from the estimated model.
2e. If the two data sets are not sufficiently similar, a new model is estimated and the process repeated. If the two data sets are sufficietly similar, we can proceed to the next step in the process.
This set of figures does not explain how each step is done, it simply outlines what is done when testing to see if the model is capable of explaining the observations (field data). Also, we have not explained what the criteria are for deciding whether two data sets are "sufficiently similar." That will be covered in the next chapter.

A crucial concept: non-uniqueness

The other decision involves a more subtle issue. For most inversion problems that will be discussed in this work, we will have digitized the Earth with more cells than we have data values. Therefore, it will be impossible to find a unique value for each cell without additional information. This issue is referred to as the problem of non-uniqueness. All problems like this are called "under-determined," and it is common to say that they have non-unique solutions. That is, all problems with more unknowns than data will have an infinite number of possible solutions. Furthermore, there will be errors associated with every data point, making the problem even more difficult to solve.

Parametric problems: Situations when there are fewer parameters describing your model than there are measurements are called "over-determined" problems. They are usually dealt with in a completely different manner, but interpretation of over-determined problems is also non unique. For example, if a particular geometric shape is assumed in the parametric solution (a buried cylinder perhaps) one unique solution will be recoverable. However a different parameterization could be invoked - perhaps a buried multi-sided object - so the interpretation is in fact non-unique. See Section 4.6 for more discussion of parametric problems. The main point here is that, because we want the flexibility of explaining as much of the true complexity of the 3D Earth as possible, non-uniqueness is a pervasive characteristic of solving the geophysical inverse problem.

The next figures illustrate non-uniqueness for under-determined problems, when the Earth is divided into many more cells than there are data values. The data set on top is a synthetic magnetics data set generated by measuring the fields on the surface above a cube of magnetic material buried between the depths of 50m and 75m. Applying inversion with this data set means trying to determine what distribution of magnetic material caused the data.

Two aspects of non-uniqueness have been mentioned (that this is an under-determined problem, and that data are noisy), and there is also sometimes a third aspect. Some physical measurements do not contain adequate information. For example, potential fields data (including magnetic and gravity surveys) do not contain information about the distance between the cause and the effect. In other words, as illustrated in Figure 3 above, it is possible to generate any data set with a thin layer of material if the particles can take on unlimited values of the relevant physical property. The problem is further illustrated with a hypothetical gravity survey shown in Figure 3e below.

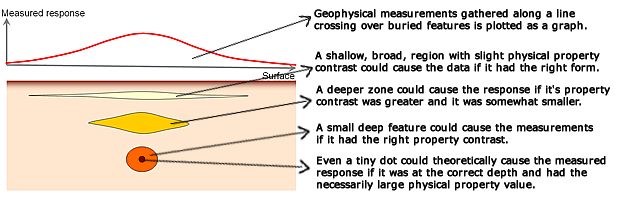
Figure 3e: Measured response of a gravity survey along a survey line (in red) over four different models. All four models are equally capable of causing the data, and the data contain no information about which of the four models is the true model.

Resolving this aspect of non-uniqueness requires modifications to the general solution, as explained in the section entitled "Mods for mag/grav" in Chapter 4 "Inversion theory".

Decision number 2: Optimal model

How does the issue of non-uniqueness relate to decision number two, which relates to whether the model is an optimum one. Since an infinite number of models are possible, alternative information must be used to constrain the models so that one can be chosen in favour of all the rest. This is where prior information (what we already know about the problem) comes in. What do we know? In other words, what constitutes prior knowledge? Regardless of how much or how little work has been done at the field site, a significant amount may be known about the geoscience problem. Here are examples:

• There will be geological information. For instance, it may be known that background rocks hosting the target are non-magnetic (limestone for example). It may be known that there is non-magnetic overburden that is at least a few metres thick. The basic structural situation may be reasonably well understood from surface mapping and other work.
• There will be geophysical information. For example, we know that magnetic susceptibility must take on positive values. Density contrasts, on the other hand, may be either positive or negative depending upon whether "target" materials are more or less dense than host materials.
• There will be logical information. For example, it is sensible to look for a "simple" solution. It will be possible to find an arbitrarily complicated model to explain the data but it will NOT be possible to find an arbitrarily simple solution if there is any pattern to the data set. Therefore it makes sense to look for the simplest model that can explain the data. "Simple" may mean as little structure as possible, or as little departure from an initial structure as possible, or a structure that is as smooth as possible.

Selection of an "optimum" model means constraining the infinite number of solutions to those that are consistent with what we already know or assume about the situation. Exactly how this prior information influences the inversion process is discussed in detail in the next chapter.

Usable results

Displaying and using 3D results of inversion often takes care. It is rather easy to give the wrong impression about the result if the model cannot be examined visually in a convenient and versatile manner.

The next figures show the model obtained by inverting the data set shown in Figure 3 above, using a method that allows susceptibility to occur with equal likelihood anywhere in the volume.

4a. The data set is shown above an isosurface image of the susceptible zone recovered.
4b. An isosurface is an image with all cells with values less than some chosen cutoff value hidden from view. The choice of cutoff significantly affects the appearance of the model.
4c. Alternatively, a slice through the volume can be displayed with the cell value coded by colour. This gives a correct impression of the range, and distribution pattern, of values in the mode.
4d. , 4e. , 4f. It can be useful to display slices through the volume in several directions.
4g. A combination may be useful, and the direction used to view the model may contribute to understanding the model that has been recovered.

Summary - the fundamental flow chart

General problems

What is needed to invert a data set? This flow chart summarizes the requirements for proceeding with inversion of geophysical data for general problems. The flowchart for parametric problems is shown by rolling the mouse over the chart, and is described later in this section. The introductory page for the next chapter is an interactive version of this chart which provides details for each portion. For the present, it is sufficient to introduce the chart, and to summarize the procedure for implementing inversion as follows: Given: In order to obtain models of the subsurface by inversion, it is necessary to start with field data, estimates of errors and noise on those data, a forward modelling calculation procedure, and well described prior information or assumptions about the situation. Discretize: Describe the earth by dividing it into cells, each with fixed size and unknown but constant value of the relevant physical property. (There are other ways of describing your model of the earth, but this CD-ROM focusses on the use of rectangular cells.) Choose decision criteria: The choices made for how data predictions and survey measurements are compared, and how an optimal model is chosen (based upon prior information) are crucial for obtaining useful results.

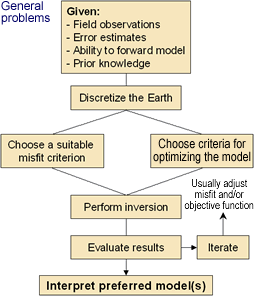• Inversion: Find values for cells which are consistent with both the measured data and the prior information. The inversion process is implemented using mathematical optimization theory.
• Evaluate the inversion result: Use a comparison between predicted data and field measurements, and take into account what is known or expected about the earth's properties and structures.
• Iteration is inevitable: No initial outcome should be used without exploring a range of equally possible models.
• Interpret the result: models of physical properties must be interpreted in terms of useful geologic or geotechnical parameters. The models must be easy to understand and convenient to manipulate.

Parametric problems

As mentioned above, when there are fewer parameters than data values, the problem does not involve choosing from an infinite variety of potential models - adjusting parameters until the model can reproduce the data as closely as possible is sufficient. Mouse over on the chart to see how the procedure changes in this case. The procedures for parametretic problems are described in greater detail in subsequent chapters.

As the theory of inversion is developed in subsequent sections, it will become clear that the primary difficulties are that the solution is non-unique, and that the necessary mathematical procedures are computationally demanding.