Exercise 2 - Calculation of Vertical Dynamic Ocean Modes

Based on https://github.com/sea-mat/dynmodes/blob/master/dynmodes.m by John Klinck, 1999.

The goal is to calculate and explore the vertical dynamic modes using a Python function that calculates numerical solutions of the generalized eigenvalue problem expressed by:

(1)\[\frac{\partial^2}{\partial z^2} w_m + \alpha^2 N^2 w_m = 0\]

with boundary conditions of \(w_m = 0\) at the surface and the bottom.

Variables:

  • \(z\) is the vertical coordinate, measured in \([m]\)

  • \(w_m\) are the vertical velocity modes

  • \(N^2\) is a profile of Brunt-Vaisala (buoyancy) frequencies squared \([s^{-2}]\)

  • \(\alpha^2\) are the eigenvalues

Your assignment:

_images/aims_allen_exercise_2.png

Get the Python Code

Open up a terminal window and an editor, and go to the dynmodes directory.

Please see the Get the Python Code section in Exercise 1 if you haven’t already cloned the AIMS-Workshop repository from GitHub.

Change to the AIMS-Workshop/dynmodes/ directory and start ipython with plotting enabled.

The Python functions we’re going to use in this exercise are in dynmodes.py.

The dynmodes() Function

The dynmodes() function has the following docstring that tells us about what it does, its inputs, and its outputs:

dynmodes.dynmodes(Nsq, depth, nmodes)[source]

Calculate the 1st nmodes ocean dynamic vertical modes given a profile of Brunt-Vaisala (buoyancy) frequencies squared.

Based on https://github.com/sea-mat/dynmodes/blob/master/dynmodes.m by John Klinck, 1999.

Parameters:

  • Nsq (numpy.ndarray) – Brunt-Vaisala (buoyancy) frequencies squared in [1/s^2]

  • depth (numpy.ndarray) – Depths in [m]

  • nmodes (int) – Number of modes to calculate

Returns:

(wmodes, pmodes, rmodes, ce) vertical velocity modes, horizontal velocity modes, vertical density modes, modal speeds

Return type:

tuple of numpy.ndarray

Analytical Test Cases

For unit depth and uniform, unit \(N^2\) the analytical solution of the (1) is:

\[w_m = w_o \sin(\frac{z}{ce})\]

where

\[ce = \frac{1}{n \pi}\]

and \(w_o\) is an arbitrary constant, taken as 1.

Calculate the 1st 3 dynamic modes for this case using dynmodes():

In []: import numpy as np

In []: import dynmodes

In []: depth = np.linspace(0, 1, 21)

In []: Nsq = np.ones_like(depth)

In []: wmodes, pmodes, rmodes, ce = dynmodes.dynmodes(Nsq, depth, 3)

In []: ce
Out[]: array([ 0.31863737,  0.15981133,  0.10709144])

Calculate the 1st 3 modes of the analytical solution for this case:

In []: const = 1 / np.pi

In []: analytical = np.array((const, const / 2, const / 3))

In []: analytical
Out[]: array([ 0.31830989,  0.15915494,  0.1061033 ])

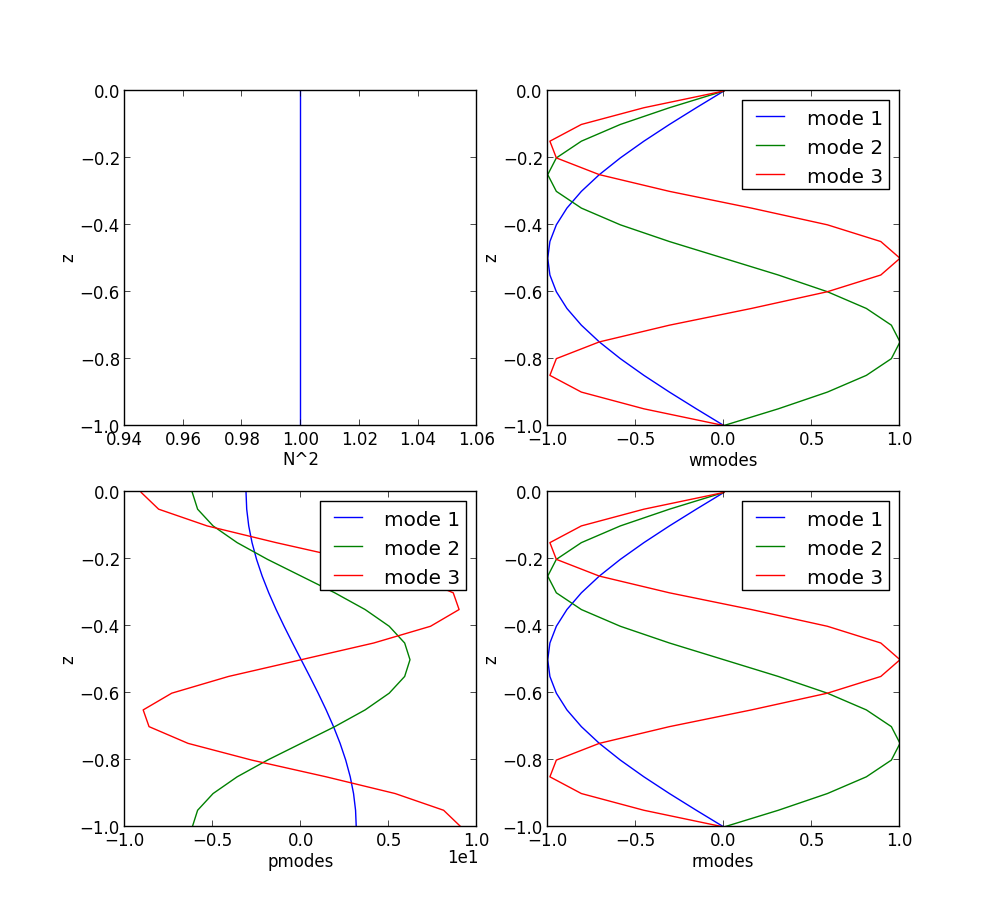
Finally, plot \(N^2\) and the vertical and horizontal modes, and the vertical density modes:

In []: dynmodes.plot_modes(Nsq, depth, 3, wmodes, pmodes, rmodes)
_images/analytical_case1.png

Another case with an analytical solution that you can try is:

  • 400 \(m\) depth at 10 \(m\) intervals

  • Uniform \(N^2 = 1 \times 10^{-6} \ s^{-2}\)

The analytical solution is:

\[w_m = w_o \sin(\frac{N z}{ce})\]

where

\[ce = \frac{N H}{n \pi}, N = 1 \times 10^{-3} \ s^{-2}, H = 400 \ m\]

Exploring Different Stratifications

There are 4 density profile files for you to explore:

  • SoG_S3.dens is from the Strait of Georgia on the west coast of Canada

  • s105.dens and s109.dens are from Florida Straits

  • so550.dens is from the South Atlantic offshore of Cape Town

The dynmodes.read_density_profile() function will read those files and return depth and density arrays. You can view its docstring via the ipython help feature:

In []: dynmodes.read_density_profile?

The dynmodes.density2Nsq() function will convert a density profile to a profile of Brunt-Vaisala (buoyancy) frequencies squared.