EOSC 450
Potential Fields in Earth and Planetary Sciences
Course Overview
Lecture Notes
Problem Sets
0. Overview notes from first class
A. Introduction to potential theory
1. Introductory material: fields, potential, Laplace's equation, harmonic functions, delta-functions
2. Mathematical background: Green's Functions, Helmholtz Theorem, Green's Identities
* some additional notes on Green's functions
* additional notes on an application of Gauss's Law
* Green's Equivalent Layer Theorem
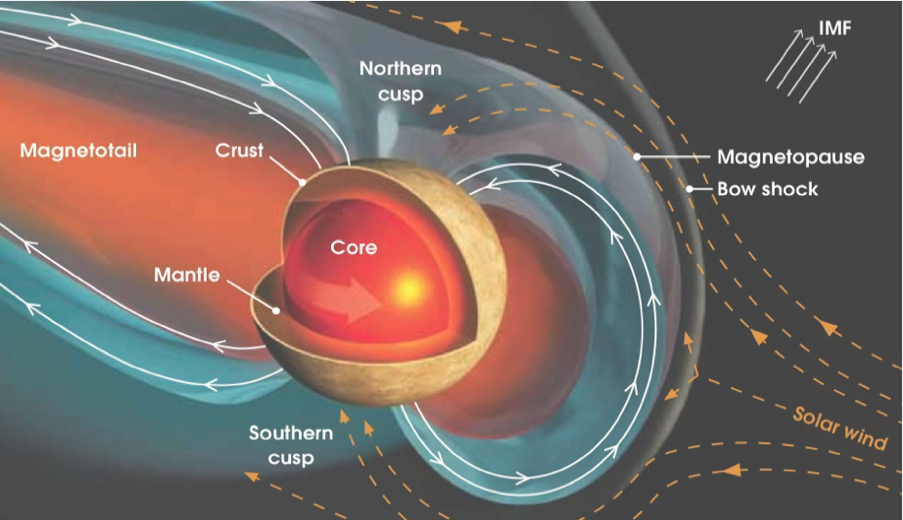
4. Introduction to magnetics
* Magnetic potential (vector and scalar) and magnetic induction (Blakeley, ch. 4)
* Magnetization (Blakeley, ch. 5)
* Magnetic susceptibility of rocks
* Magnetics: A few forward problems
B. Overview of tools needed
1. Fourier Transforms
* Summary notes from Doug Oldenburg via Mark Jellinek.
* Some additional notes with pictures....
* MATLAB code:
- Catherine Johnson's demo script
- The Never-Lose-This-Because-It's-The-How-To Matlab script based on
http://blogs.uoregon.edu/seis/wiki/unpacking-the-matlab-fft/
2. Solutions to Laplace's equation
3. Upward/downward continuation - example using martian magnetic field - slides
* In-class exercise and the coeffiecients you need.
C. Gravity, isostacy and flexure
1. Global Gravity - Reference Surfaces and Summary Notes
2. J2; Moments of Inertia
3. Geoid, Free Air Gravity and Bouguer Gravity
4. Isostacy and slides from Catherine Johnson
5. Flexure
6. Gravity/Topography admittance
D. Magnetic fields and magnetization
1. Global planetary magnetic fields
2. Marine magnetic anomalies
Potential theory is used widely to analyze problems involving gravity, magnetics, heat and fluid flow. Applications of potential methods in the Earth, ocean, atmospheric and planetary sciences are include geophysical exploration, satellite altimetry, the mechanical properties of planetary lithospheres, the structure and secular variation of the Earth's magnetic field, the magnetic fields of other solar system planetary bodies, flow in the atmosphere, flow of groundwater, Milankovitch cycles (orbitally-forced ice ages), and the tidal triggering of earthquakes and moonquakes. In this class we will develop the theory of potential methods, along with the essential tools needed to analyze real data sets. We will address selected topics in class, as homework problems and in final projects.
Essential Course Information: (subject to change) Overview / Assessment etc
Course Schedule: Week-by-week. Note that this is subject to change (including due dates for assignments and quizzes) at the discretion of the instructor. Upcoming deadlines will be announced in class or/and via email.
Meeting Times / Location: Tu/Th 2:00-3:30 pm, EOS Main 105


Instructor
Manar Al Asad
malasad@eoas.ubc.ca
EOS-M 302
TA
Megan Russell
mrussell@eoas.ubc.ca
EOS-M 302
General advice for doing problem sets successfully
1. Math review.
2. Gravity inside planets
3. Magnetic field modeling I: Dipoles. You'll need the problem set, magdip.m and dipm2b.m
4. Fourier transforms: review and MATLAB implementation.